In deze miniserie getiteld ‘Dansende deeltjes’ beschrijven we drie manieren waarop het getal van Avogadro is bepaald. In het eerste deel zagen we dat hele kleine stuifmeelkorreltjes in water zich net zo gedragen als de moleculen in de lucht: des te hoger je in zo’n suspensie komt, des te lager de concentratie van de stuifmeelkorreltjes wordt. Hetzelfde gebeurt met de concentraties van stikstof, zuurstof en dergelijke als je hoger in de lucht komt. Uit dit fenomeen kon Jean Baptiste Perrin in 1909 de constante van Boltzmann bepalen, en daarmee het getal van Avogadro: . In deze formule is R de gasconstante die wel bekend was.
Brownse beweging
In 1828 zag botanist Robert Brown dat er in de vacuoles (blaasjes gevuld met vloeistof) van stuifmeelkorrels iets zat, dat continu bewoog. Eerst dacht hij dat dit kwam doordat de stuifmeelkorrels op een of andere manier ‘levend’ waren. Echter, ook de stuifmeelkorrels van een plant die meer dan 100 jaar dood was, vertoonden dit vreemde gedrag. Ook niet-organisch materiaal zoals hele kleine glaskorreltjes vertoonde deze merkwaardige beweging. Met leven kon het dus niks te maken hebben. Maar waarmee dan wel?
Het duurde zeker nog tot 1905 voordat Einstein met een bewijs kwam. De beweging werd veroorzaakt door de moleculen van het oplosmiddel (bijvoorbeeld water) die tegen de deeltjes aanbotsen. Daardoor leggen de deeltjes een zogeheten ‘random walk’ af: ze zetten iedere keer een ‘stap’ in een willekeurige richting, net als een dronken student.
De simpelste random walk is in één dimensie, dus op een rechte lijn. Stel dat we met één deeltje op het punt beginnen, en we verplaatsen het steeds met een even grote stap naar links of rechts. We spreken af dat ‘-1’ een stap naar links is, en ‘+1’ een stap naar rechts. De kans op ‘-1’ of ‘+1’ is even groot. De nieuwe positie wordt
, waarbij
elk willekeurig +1 of -1 zijn. In onderstaande afbeelding zie je een random walk in 2 dimensies.
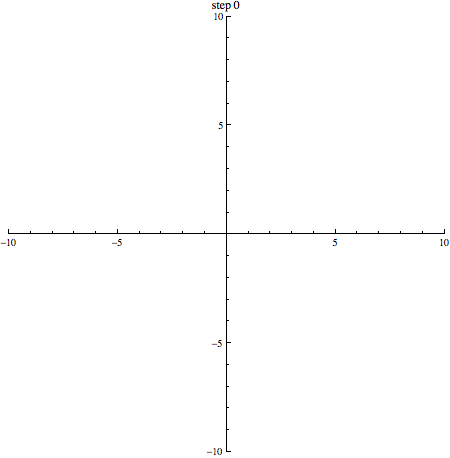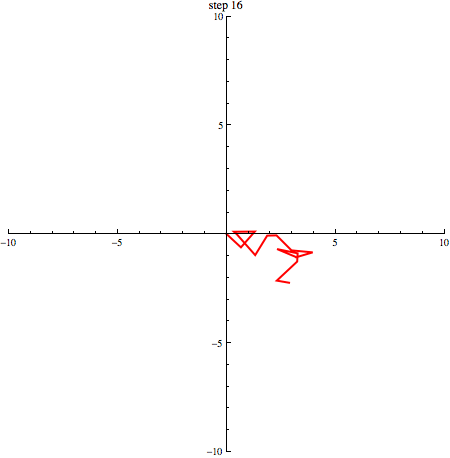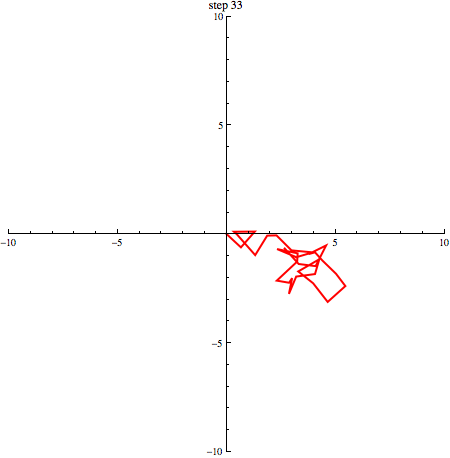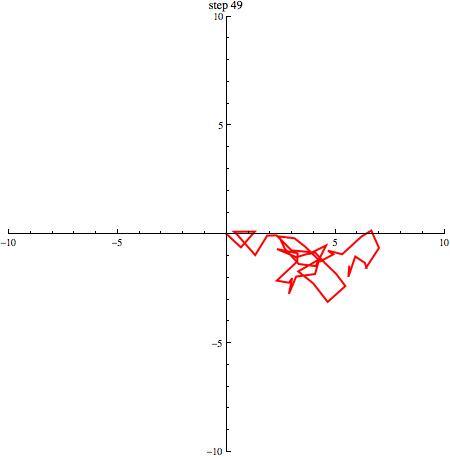
Als we een aantal stappen zetten met heel veel deeltjes, verwachten we dat we even vaak naar links en naar rechts stappen. Gemiddeld genomen verplaatsen de deeltjes zich dus niet. We kunnen schrijven: . De haakjes om de x geven aan dat het hier om een gemiddelde gaat. Dat zie je in onderstaand plaatje (1000 deeltjes die zich volgens een random walk verplaatsen, beginnende in de oorsprong): de vlek breidt zich steeds verder uit, maar het middelpunt blijft op zijn plek.
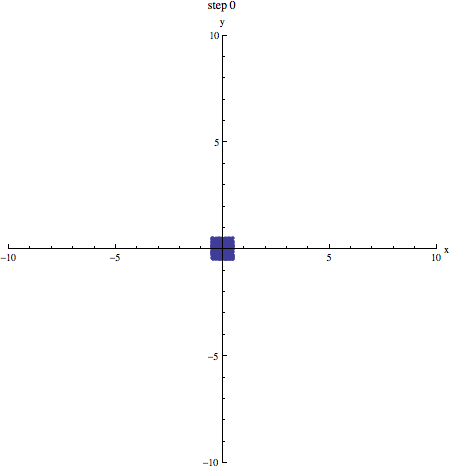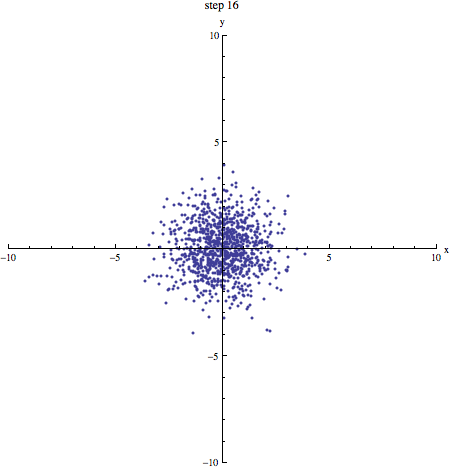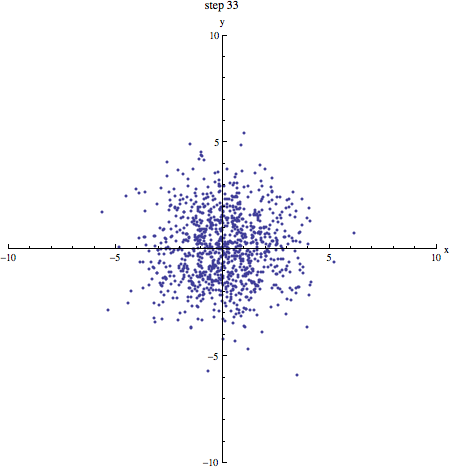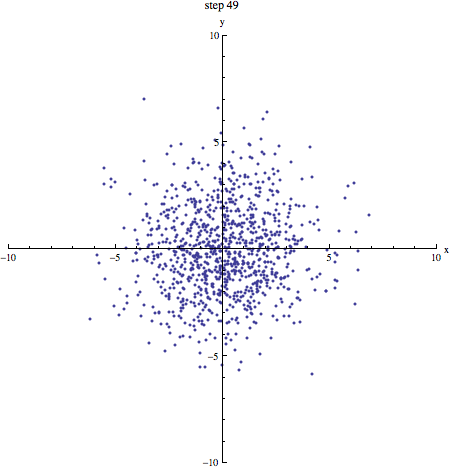
In bovenstaand plaatje zie je duidelijk dat de vlek steeds groter wordt: de random walk van moleculen is de basis voor diffusie! Een maat voor (het kwadraat van) de grootte van de vlek na een bepaald aantal stappen is . Omdat
altijd positief is, is dit gemiddelde wél groter dan nul. Voor een random walk als hierboven kan men laten zien dat
, of dat
. N is hierin het aantal gezette stappen, en b is de stapgrootte (b = 1 in ons geval).
Als je nog steeds wakker bent, zul je je waarschijnlijk inmiddels wel afvragen: “wat heeft dit in hemelsnaam te maken met het getal van Avogadro?” Daar komen we nu. Voor ronde deeltjes in een oplosmiddel geldt een soortgelijke formule: (voor twee dimensies). In plaats van het aantal stappen N hebben we nu de tijd t, en op de plaats van de stapgrootte staat nu de Einstein diffusiecoefficient D. Einstein liet als eerste zien dat
. Hierin staat weer de Boltzmannconstante kB, samen met de absolute temperatuur T. η is de stroperigheid, of liever: de viscositeit van het oplosmiddel. r is de straal van het bolvormige deeltje.
Wat Jean Baptiste Perrin deed, kun je nu waarschijnlijk wel raden. Door van heel veel colloidale deeltjes onder een microscoop de afgelegde route/afstand te meten, kon hij bepalen.
Daaruit berekende hij de diffusiecoefficiënt, en daarmee de Boltzmannconstante kB. Via de bekende gasconstante rekende hij het getal van Avogadro uit: . Hij kwam uit op
. Ook niet slecht. Het is daarom zeker het vermelden waard dat Jean Baptiste Perrin voor zijn werk in 1926 de Nobelprijs heeft gekregen.

Mooi gemaakt Mark, met die filmpjes!
Ik vind het wel vreemd dat uit zo’n formule precies het aantal koolstofatomen volgt dat een massa levert van 12 g. Dat kan geen toeval zijn. De reden ligt waarschijnlijk in hoe de gasconstante R bepaald wordt. Het zou leuk zijn als je dit een volgende keer behandelde.
Dat is inderdaad beslist geen toeval, dat is zo afgesproken. De atomaire massa-eenheid (u) is een relatieve schaal. Een koolstof-12 atoom is ongeveer 12 keer zo zwaar als een waterstof-1 atoom. Er is afgesproken dat een koolstof-12 atoom een massa van 12 u heeft, of equivalent dat 1 u een twaalfde deel is van de massa van het koolstofatoom.
De constante van Avogadro is zo gedefinieerd dat een mol van een object met massa 1 u, 1 gram geeft. Een mol koolstofatomen is dus per definitie 12 gram.
Dat moet inderdaad verwerkt zitten in de gasconstante; precies via . De gasconstante is gewoon de per mol versie van de Boltzmannconstante (per molecuul). Als we een andere definitie van de mol hadden (bijvoorbeeld omdat we ‘1 u’ anders hadden gedefinieerd), zou denk ik de gasconstante een andere waarde hebben, maar de Boltzmannconstante niet. Dit kun je zien aan bijv de twee equivalente versies van de ideale gaswet,
. De gasconstante is gewoon de per mol versie van de Boltzmannconstante (per molecuul). Als we een andere definitie van de mol hadden (bijvoorbeeld omdat we ‘1 u’ anders hadden gedefinieerd), zou denk ik de gasconstante een andere waarde hebben, maar de Boltzmannconstante niet. Dit kun je zien aan bijv de twee equivalente versies van de ideale gaswet,  en
en 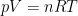 . Als we het aantal mol anders gaan definieren, verandert R zodanig mee dat
. Als we het aantal mol anders gaan definieren, verandert R zodanig mee dat 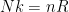 blijft kloppen.
blijft kloppen.
Ik ben wel heel erg benieuwd hoe men in die tijd de gasconstante heeft kunnen meten; dat zou ik namelijk niet weten. Heb jij daar nog ideetjes over, Freddy?
Nee, ik weet het niet.
Als ik de kans krijg, zal ik het eens aan Albert Philipse vragen. Die hoort dat toch te weten…
Bij nader inzien is het niet eens zo moeilijk om de gasconstante te bepalen uit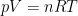 zonder dat je de constante van Avogadro kent. Laten we stikstofgas, N2, als voorbeeld nemen. Wat je kunt doen is het gas wegen. Als je 28 gram gas hebt, heb je (per definitie) 1 mol gas. De temperatuur, druk en volume kun je meten. Hieruit volgt dus direct de gasconstante. Je moet wel de relatieve atoommassa’s weten, maar ik heb geen idee hoe lang die al bekend zijn.
zonder dat je de constante van Avogadro kent. Laten we stikstofgas, N2, als voorbeeld nemen. Wat je kunt doen is het gas wegen. Als je 28 gram gas hebt, heb je (per definitie) 1 mol gas. De temperatuur, druk en volume kun je meten. Hieruit volgt dus direct de gasconstante. Je moet wel de relatieve atoommassa’s weten, maar ik heb geen idee hoe lang die al bekend zijn.
De relatieve atoommassa’s heeft Dalton volgens mij voor het eerst bepaald. Hoe dan ook, totdat men zeker wist dat water [latex]H_{2}O[/latex] is, had men ook nog problemen met of water nou 8 u of 16 u is. Dalton had al een vrij geavanceerd systeem om moleculen te tekenen (hij hield in het begin aan dat water [latex]HO[/latex] was).
Relatieve atoommassa’s moet je weten ja, en molecuulformules. Vroeger was het getal van Avogadro gedefinieerd als het aantal atomen zuurstof-16 in 16 g (bron: Wikipedia). Dat doet vermoeden dat de gasconstante werd bepaald door pV/nT voor zuurstof (O2-gas) te meten.