Periodiek systeem (niet) compleet met 113, 115, 117 en 118

De ontdekking van elementen 113, 115, 117 en 118 is volgens het IUPAC bevestigd. Is daarmee nu het periodiek systeem der elementen compleet? Omdat wij ook niet van clickbait houden: nee. Maar waarom zijn chemici en natuurkundigen dan tóch heel blij? En hoe reëel is het nu dat er nog nieuwe elementen worden ontdekt?

Mijn professor organische chemie zei vroeger altijd: “Scheikundigen doen het met elektronen.” Als dat zo is, dan doen natuurkundigen het met protonen. Ik zal hieronder uitleggen waar ook alweer het periodiek systeem der elementen vandaan komt, en waarom scheikundigen deze vorm zo gemakkelijk vinden.

De atoomkern

Eerst even een opfrisser: een atoom heeft een kern met daarin zware protonen. Heeft het atoom 1 proton, dan noemen we het ‘waterstof’, heeft het 2 protonen, dan heet het ‘helium’, 3 ‘lithium’, etcetera. Dit is het allerbelangrijkste dat je moet onthouden van dit hele verhaal. De nieuwe elementen die zijn ontdekt hebben hebben ‘atoomgetallen’ 113, 115, 117 en 118. Dat zijn precies die aantallen protonen in de atoomkern. Hoppa.

Wat is er nou zo speciaal aan die kernen? Daar zitten dus die protonen in, en (bijna) even zware neutronen. Dat moet ook wel, want die protonen zijn elektrisch geladen. Ze zijn namelijk positief. Waarom ze niet uit elkaar spatten door al die lading zo dicht op elkaar? Grotendeels vanwege de neutronen en de sterke kernkrachten. Die houden de protonen en neutronen bij elkaar, ondanks dat de positieve lading van de protonen het zaakje uit elkaar wil duwen: een delicate balans.

Nu de vorm van het periodiek systeem. Dat is vanwege de elektronen. Omdat een proton 1 positieve lading heeft, en een elektron 1 negatieve lading, moeten er evenveel elektronen om een kern heen vliegen als dat er protonen in zitten. Die elektronen tekenen we altijd alsof ze in rondjes rond de kern zweven (zoals in het Born-model), maar eigenlijk is dat niet helemaal waar. Al maakt het het verhaal wel een stuk eenvoudiger uit te leggen. Om dit te begrijpen betreden we de wereld van de kwantummechanica. Wil je natuurkundestudenten laten huilen? Vraag of ze de Schrödingervergelijking voor drie lichamen willen oplossen. (En ik huil met hen mee).

Pauli’s regel en de elektronen

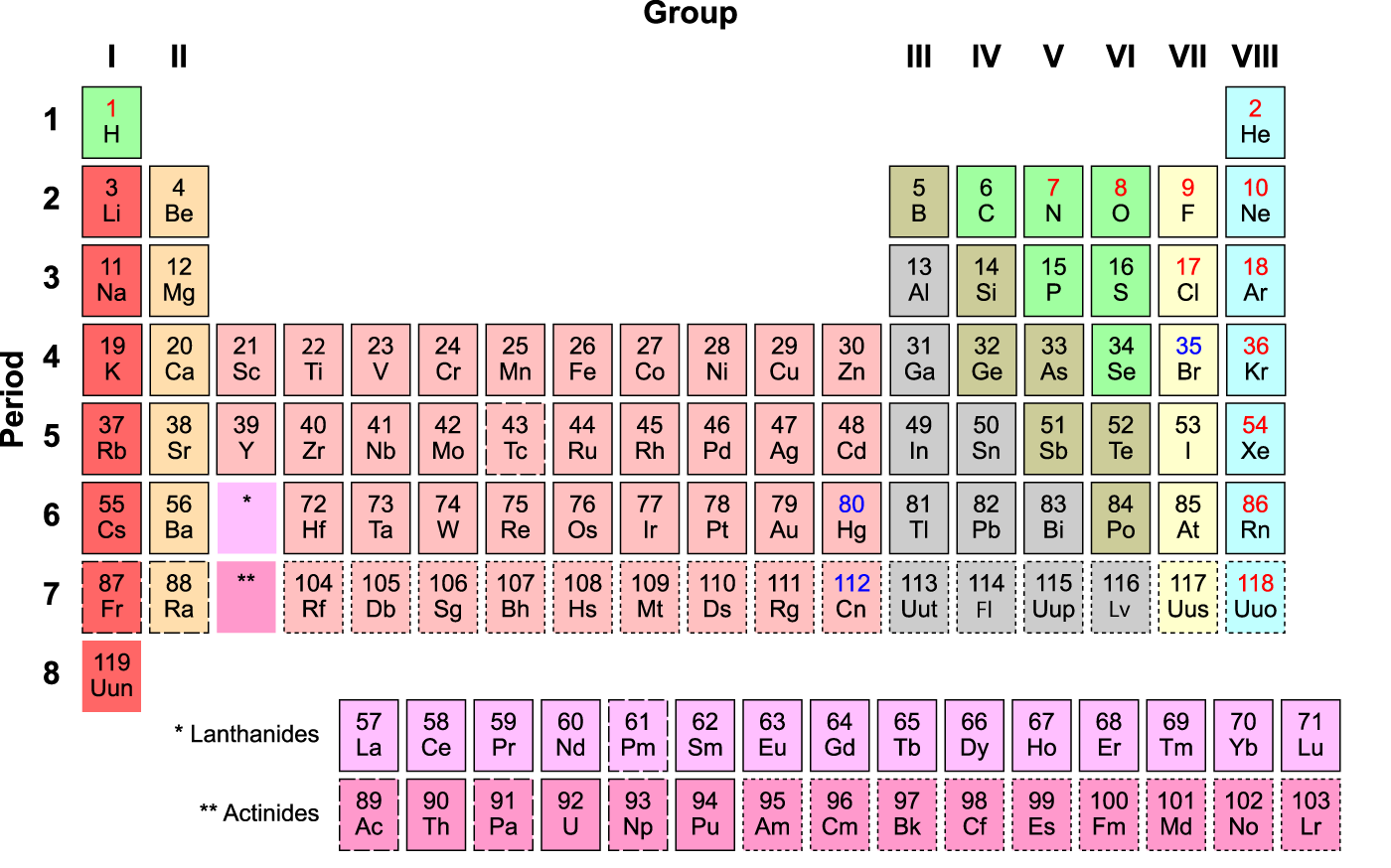
Hoe dan ook, die elektronen rondom de kern zitten daar niet gewoon thee te drinken. Die hebben een leven op zich, dat bepaald wordt door strenge regels. Een van de regels is die van Pauli. Pauli’s regel zegt dat elektronen niet zomaar met z’n allen hetzelfde kunnen gaan zitten doen. Daarom rangschikken de elektronen zich rondom een atoom in een nauwgezette ordening die bepaalt waarom het periodiek systeem der elementen eruit ziet zoals hierboven.

Elektronen schikken zich in schillen, net zoals een ui schillen heeft. Elke schil heeft een vorm en een nummer. Omdat er nogal wat wiskunde bij komt kijken, hebben die vormen namen die lekker kort zijn: s, p, d, f, enzovoorts. Don’t ask. De eerste schil heet 1s, de tweede 2s, dan komt 1p, dan 2p, 3s, (wordt je al gek?), 3p, 4s, 3d, en zo nóg een heleboel meer. Waarom die volgorde zo raar is? Maakt nu even niet uit. Maar wel wèl uitmaakt is dat er in s-schillen 2 elektronen passen, in een p-schil 6 en in d-schillen 10. Als we deze getallen nu eens naast het periodiek systeem leggen, kun je overeenkomsten vinden.

De vorm van het periodiek systeem

Als je nu nog niet afgehaakt bent, pak dan gerust eens even een periodiek systeem, dan verklap ik het. Als we vanaf linksboven kijken, zien we dat waterstof 1 elektron heeft. Die eerste gaat in de 1s-schil. Helium heeft 2 elektronen, die allebei in de 1s schil passen. Lithium heeft 3 protonen, dus 3 elektronen, waarvan er 2 in de 1s-schil passen, en 1 in de 2s. Beryl­lium stopt z’n elektronen in de 1s èn de 2s-schillen. Nu komt het interessante: boor. Boor is het eerste element dat een elektron in de 2p-schil stopt. En alle elementen tot en met neon doen hetzelfde. Daarna doen natrium en magnesium wat in de 3s-schil, waarna aluminium weer wat in p-schillen stopt. Okay, dit is echt veel teveel tekst. Kom, hier is een plaatje met wat ik bedoel:

Nu is het gemakkelijk om te zeggen “Ja maar Aldo, eerst vertel je zo ingewikkeld dat elektronen zo raar opvullen en daarna laat je die afbeelding zien. Als je het andersom had verteld, was het veel gemakkelijker.” Okay, dat zeg je niet, want het is nog steeds heel ingewikkeld. Wat je moet begrijpen is dat er een natuurkundige was die Pauli heette, veel moeilijke wiskunde en de kwantummechanica, die samen voorspellen hoe elektronen zich bezig houden rondom een atoomkern. En dat die voorspelling heel goed overeen komt met hoe het periodiek systeem der elementen eruit ziet. Dit zijn de overwinningen in de wetenschap: eerst een voorspelling doen, en later kunnen bevestigen met experimenten en observaties.

Herinner je dat de Russische natuur- en scheikundige Dmitri Mendeleev in de negentiende eeuw bedacht dat het periodiek systeem deze vorm moest hebben. Van kwantummechanica was toen nog geen sprake.

Balletjes van protonen en neutronen

Nog een laatste vraagje op het nieuws: nu zijn elementen 113, 115, 117 en 118 ontdekt. Maar die daar tussenin dan? Wat is er zo speciaal aan elementen 112 en 116? Dat heeft te maken met hoe je een balletje van balletjes kan maken, en de elektronen die eromheen vliegen. Over die balletjes van balletjes: stel je voor je hebt een grote hand magnetische knikkers die elkaar aantrekken. Als je drie van die magnetische knikkers tegen elkaar aan drukt, kunnen die op 2 manieren tegen elkaar: in een driehoekje en in een sliertje. Maar we snappen allemaal dat zo’n sliertje al snel in elkaar stort tot zo’n driehoekje. Vier van die magnetische knikkers zullen graag in een soort kubus-achtig figuurtje zitten (een tetrahedron). Die is heel stabiel. Als we nu een vijfde knikkertje toevoegen, valt die een beetje buiten dat blobje van vier. Als we meer en meer knikkers toevoegen, zal al snel blijken dat (na een beetje schudden en herschikken) sommige vormpjes heel erg dichtgepakt zullen zijn, terwijl het toevoegen van nóg een knikker een beetje rommelige, instabiele structuur geeft. Die meest stabiele structuren hebben een ‘magisch’ aantal knikkers: 2, 8, 20, 28, 50, 82, 126, 184, enzovoorts. Het laatst-toegevoegde balletje bij 21 knikkers zal dus bijvoorbeeld heel losjes op de bol van 20 knikkers zitten.

Dit is waarom atoomkernen vanaf rondom 82 en 126 protonen opeens een stuk minder stabiel zijn. (Voor de connaisseurs, kijk naar dit plaatje). Wat is er nou zo speciaal aan elementen 112 en 116, ten opzichte van elementen 113, 115, 117 en 118? Er is een fijne balans tussen hoe die balletjes van protonen en neutronen stabiel zijn, en die elektronen die de boel ook nog eens een beetje bij elkaar houden. Elementen 112 en 116 zijn relatief iets stabieler, dus waren gemakkelijker om te ontdekken.

Periodiek systeem nu compleet?

Nope. Er is geen limiet aan het aantal protonen in een atoomkern, dus er kunnen altijd meer elementen bijkomen. Al is er wel een limiet aan hoe stabiel een kern is: als een kern maar groot genoeg is, vervalt hij. Lood (82 protonen) is het laatste stabiele element; alle elementen daarna vallen spontaan uit elkaar. Het bekendste instabiele element is nummer 92: uranium. Hoe groter het aantal protonen, hoe instabieler het element. Element 112 copernicium heeft bijvoorbeeld een halfwaardetijd van ongeveer 29 seconden, terwijl naamloos element 115 een halfwaardetijd heeft van 0,2 seconden. Volgende elementen zullen alleen maar instabieler zijn, en ontdekking hangt volledig af van de stand van de wetenschap.

Lees meer

– Ontdekking van 112
– Bevestiging van 112, met voorgestelde naam copernicium
– Ontdekking van 115
– Bevestiging van 114 en 116, met een filmpje over 113, 115, 117 en 118
– Naamgeving van 114 en 116, flerovium en livermorium, resp.
– Alternatieve vormen voor het periodiek systeem der elementen
– Tweede alternatieve vorm (die beter correspondeert met ‘electron orbitals’)
– Een douchegordijn met het periodiek systeem, die uit The Big Bang Theory