Scheikundejongens

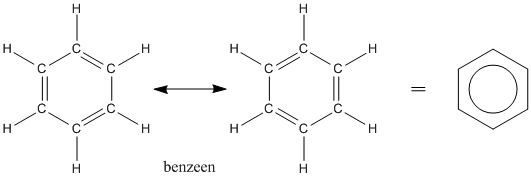
In deze miniserie beschrijven we drie manieren waarop het getal van Avogadro kan worden bepaald. In het eerste deel beschreven we hoe de barometrische hoogteverdeling het Jean Baptiste Perrin mogelijk maakte om de constante van Boltzmann te bepalen, en daaruit het getal van Avogadro via 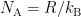. Het tweede deel legt uit hoe de Brownse beweging eveneens de Boltzmannconstante kan worden bepaald en wederom daaruit het getal van Avogadro. Dit zijn echter betrekkelijk indirecte manieren om het getal van Avogadro te bepalen. Nu zullen we naar een directere manier gaan kijken.

Deeltjes die niet dansen

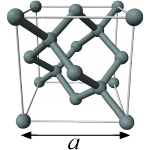
Bij deze directere manier kijken we niet naar de wanorde van dansende deeltjes, maar juist naar kristallen. In een kristal zijn de atomen (of moleculen) netjes geordend in een steeds terugkerend patroon. Dit noemen we het kristalrooster. De kleinste bouwsteen waaruit we zo’n rooster door puur te stapelen kunnen opbouwen, noemen we de eenheidscel. In het plaatje rechts zie je de eenheidscel van silicium. Het is een kubus met op de hoekpunten, op de middens van de vlakken en in de kubus siliciumatomen.

Effectief zitten er in deze eenheidscel acht silicium atomen. De acht atomen op de hoekpunten worden gedeeld door acht eenheidscellen, de zes op de vlakken door twee eenheidscellen en de vier binnen de eenheidscel horen bij maar één eenheidscel ().

De lengte van de ribbe van deze kubus heet de celribbe en heeft lengte a. Deze celribbe is (met behulp van röntgendiffractie) heel nauwkeurig en direct te meten. Zo’n eenheidscel heeft ook een volume, namelijk 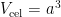. Als je bedenkt dat er in een eenheidscel acht siliciumatomen zitten, is het volume dat één atoom inneemt dus .

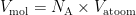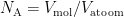
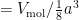
Het volume dat één mol siliciumatomen inneemt is het volume van één atoom keer het aantal atomen in een mol, oftewel het volume van één atoom keer de constante van Avogadro: . Andersom: het getal van Avogadro is het volume van een mol gedeeld door het volume van één atoom:   . Als we nu het volume van één mol zouden weten en de celribbe a zouden meten, zouden we de constante van Avogadro kunnen berekenen.

Om het volume van één mol silicium te weten moet je het gewicht van een mol kennen en de dichtheid: . Dat lijkt misschien een probleem, maar dat is het niet. De relatieve massa’s van atomen zijn erg nauwkeurig bekend. De massa van een silicium atoom is 28.0855 u. De molaire massa is daardoor per definitie 28.0855 g/mol. Samen met de dichtheid van 2.3290 g/cm³ kom je op .

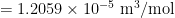Nu we het molaire volume kennen, hoeven we alleen nog de celribbe te weten. Voor silicum is deze ongeveer 0.543102 nm. Dit brengt ons het getal van Avogadro: 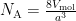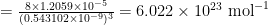. De meest nauwkeurige waarde van dit moment is 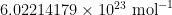, waarmee deze schatting heel goed in de buurt komt!

In deze miniserie heb je verschillende constanten voorbij zien komen: het getal van Avogadro, de constante van Boltzmann en de gasconstante. Je vraagt je nu misschien wel af: waar komen al die constanten vandaan? En hoe komt het dat ze nou die ene precieze waarde hebben? Het antwoord op die vraag is in feite heel simpel: die constantes verzinnen we zelf. Meneer Celsius en lord Kelvin hebben ooit een temperatuursschaal bedacht, zonder dat ze wisten wat er precies op de moleculaire schaal gebeurde. Nu weten we dat temperatuur te maken heeft met de (kinetische) energie van moleculen. De Boltzmannconstante is niets meer dan een getal om van het ene naar het andere te gaan. Door onze keuze voor een bepaalde temperatuursschaal, leggen we de Boltzmannconstante vast. En met onze definitie van een mol, leggen we het getal van Avogadro vast. En de gasconstante? Die ligt weer vast doordat laatstgenoemden vastliggen. En zo zijn een heleboel eenheden en constanten met elkaar verbonden.