Als iemand me zou vragen ‘Wat is chemie?’ dan zou ik iets moeten antwoorden als ‘de leer van het herschikken van atomen’.
Ik heb al eens eerder wat verteld over theoretische chemie. Die hoek — en dan vooral de kwantumchemie — van de chemie gaat dieper dan diep in, op de oorsprong van reacties. En wat is een reactie ook alweer? Het herschikken van atomen. Het breken en maken van bindingen.
Maar wat is een binding eigenlijk? Een molecuul bestaat uit atomen. Een atoom bestaat uit een kern en daar omheen elektronen. Voor het gemak kunnen we een atoom tekenen als de 2D Bohr representatie, maar die is wat lomp. Ook kunnen we een molecuul tekenen als 2D of 3D staafjes en bolletjes, maar ook die heeft wat rare implicaties. Wat er wel aan klopt is de gemiddelde locatie van de atoomkernen. En het streepje voor de binding? Sja… Er is een ‘binding’, maar een theoretisch chemicus wordt altijd wat ongemakkelijk van gewoon een streepje.
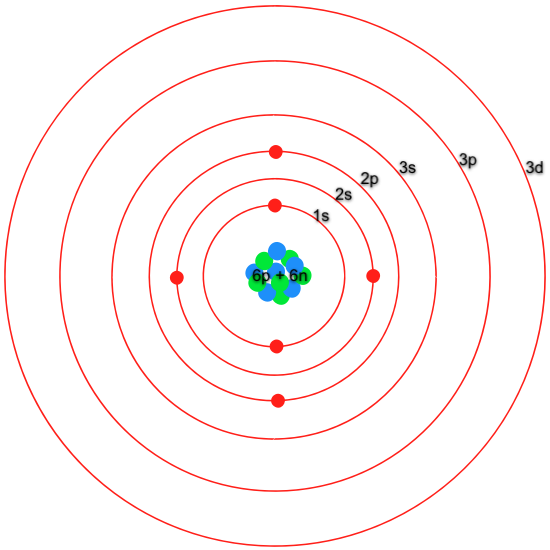
Een van de grootste gewaarwordingen uit de kwantumtheorie is dat deeltjes ook beschreven kunnen worden als golven. Je kan met de wetten van Newton de baan van een vallende knikker berekenen, dat wil zeggen, je voorspelt met behulp van wiskunde de locatie en snelheid van de knikker. Maar wat nu als die knikker geen voorwerp is, maar een golf? Als je genoeg natuurkunde en wiskunde hebt gevolgd, weet je dat golffuncties formules zijn met sinussen, cosinussen en exponenten. Het rekenen met die dingen vind ook ik altijd wat lastig, maar de dingen die je ermee kan zijn wel enorm gaaf.
Goed. De kwantumtheorie vertelt ons dat een elektron niet alleen een deeltje is, maar ook ook als golf beschreven kan worden. Als je dit lastig vindt om je voor te stellen, ga nu dan even rustig zitten. De kwantumtheorie vertelt ons ook dat we nooit zeker kunnen weten waar een elektron precies is. Of, ik moet eigenlijk zeggen, we kunnen nooit de snelheid van een elektron bepalen op een bepaalde plaats. Dus als je zegt dat een elektron ergens is, betekent dat eigenlijk helemaal niet zoveel. Maar, waar komen dan die bindingslijntjes vandaan? We kunnen toch zeggen: “Kijk, dáár is mijn elektron”?
Helaas, dat kunnen we niet. We kunnen hoogstens zeggen: “Ik weet dat het grootste gedeelte van de tijd dat het elektron dáár is”. Dat ‘daar’ is een groter gebied dan dat dunne lijntje dat je tekent.
Een theoretisch chemicus (ofwel, een kwantumchemicus) berekent waar elektronen zijn en waar ze mee bezig zijn. Hij/Zij weet dat je een elektron beter kan beschrijven als een golf. De wetten van Newton werken slecht voor voorwerpen met een kleine massa en een hoge snelheid. Als de kwantumchemicus dan ook in gedachten houdt dat een reactie (spontaan) kan verlopen als de (vrije) energie van een (gesloten) systeem verlaagd wordt, is hij eigenlijk al bijna klaar.
Is het antwoord op de vraag ‘Wat is chemie?’ nu volledig beantwoord? Ik denk het wel. Sterker nog, veel te nauwkeurig. Door de eeuwen heen hebben chemici een enorme set aan (empirische) vuistregels en minder exacte theorieën opgezet. En dat is prima, want waarom zou je willen berekenen waar de elektronen blijven, als je de baan van een vallende knikker wil berekenen?
Film van Molecular Modeling Basics